In this case the statement above the diagram is not soo handy, it becomes useful if there is something on the statement that is not included on the diagram. In that instance, we have to include it on the diagram so not to forget the piece of information.

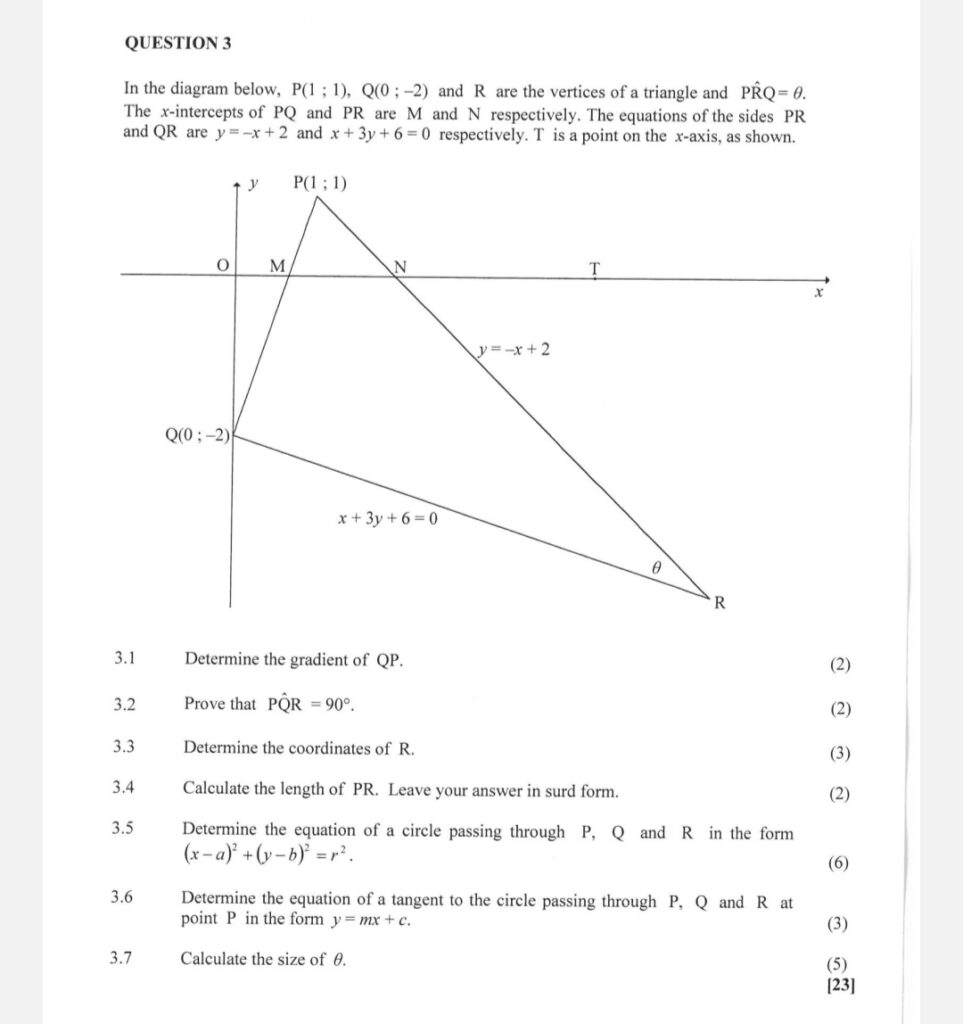
3.1

Free gradient marks, same gradient we have been doing, change in y over change in x. simple

3.2

To prove 90 degrees angle in analytical we use the product of gradients. Our job is to find gradient of PQ and QR, and multiply them to see if we get negative 1. If yes, they are perpendicular.

3.3

Looking at point R we can see that it is point of contact of the two lines with given equations, PR and QR. Make equation of QR to standard form, equate the equations and solve for x.

3.4

At this point we have both the coordinates of P and R, just substitute them into the distance formula

3.5

PR is a diameter because it subtends the 90 degree angle that we proved above.

Its half is therefore the radius, and its midpoint is the centre.

Substitute centre coordinates on a and b, do not forget to change their signs

And then sub radius and square it

3.6

To find equation of a tangent we need gradient and a point

We are given point P with both coordinates, and then ours is to find the gradient of the tangent

Tangent is perpendicular to the radius and we therefore use the product rule to find the gradient of the tangent

Use point P and R or midpoint, to find gradient of the radius

Check answer on the white board below

3.7

Angle of inclination: an angle between the x-axis and a given line

Theater is made by line QR and PR, we have to find both their inclination using their gradients.

To make it simpler, draw a dotted line representive of the x-axis since we do not have x-axis at point R

As in the board below, it can be seen that to find theater we need to subtract the angle of inclination of PR from that of QR

Answer: