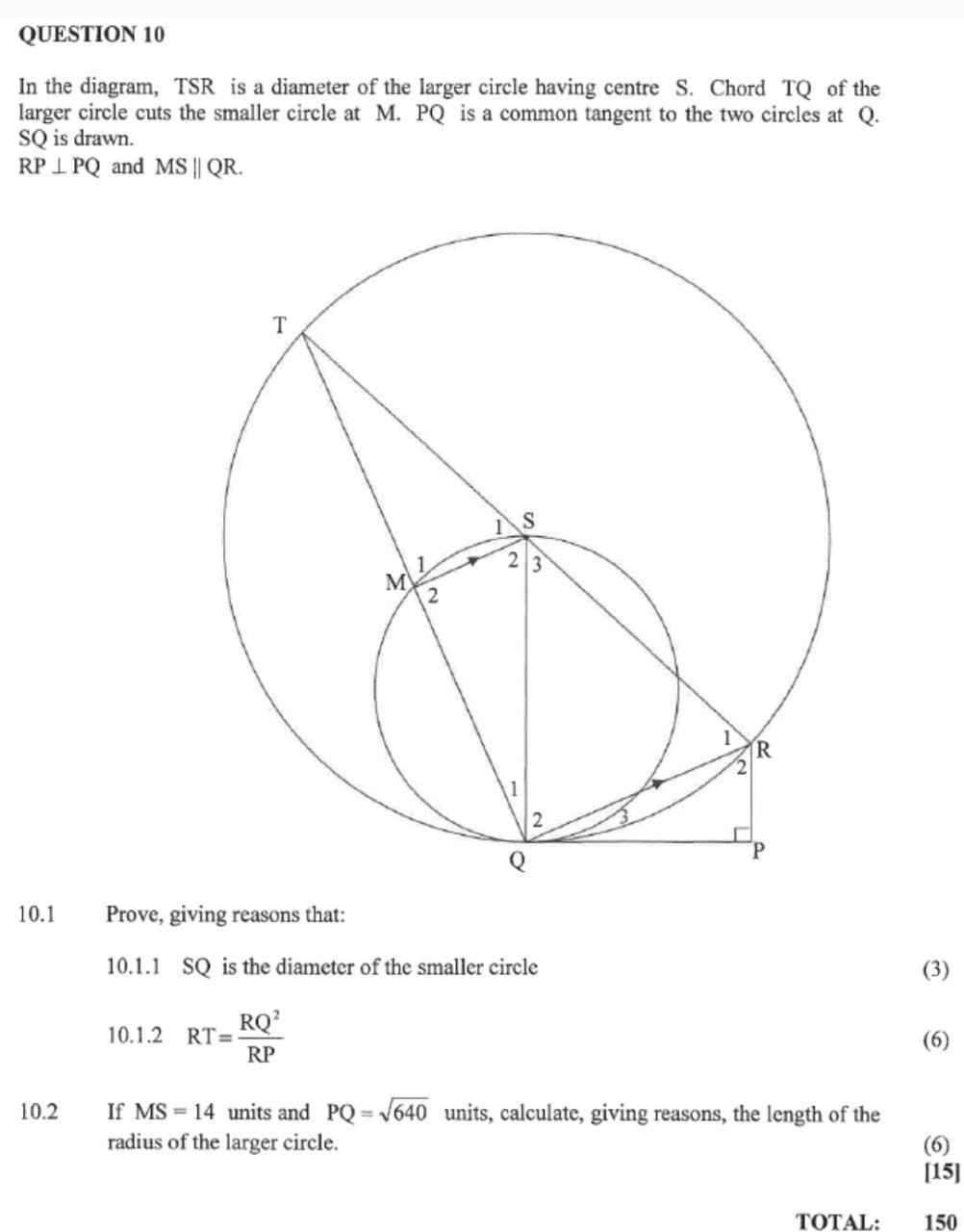
Proportionality proof:
- Draw the given proportionality triangle and connect diagonal EB and DC
- This creates triangle DEC and DEB between parallel lines DE and BC
- The area of triangle between parallel lines is equal because:
Height between parallel lines is equal
Triangle DEC and DEB share base DE
So, all the variables of the area formula are equal, the areas are therefore equal
- Create an equation, dividing area of triangle ADE by area of each triangle
- Substitute the formula and simplify.
Question adapted from DBE question paper:
- when reading the statement above your diagram, you want to highlight keywords that help you find geometry theorems
| CENTRE | TANGENT | CYCLIC QUARD | PARALLEL | PRODUCED |
| Angle at centre | Tan perpendicular to radius | Ext. angle of CQ | Alt. angles | Ext angle of CQ or triangle |
| Radii (isosceles triangle/angles opposite equal sides) | Tangents from same pt. | Opp. Angles of CQ | Corresponding | Grade 9 and 10 geometry |
| Line from centre | Tanchord | Angles on same seg. | Co-interior | |
| Diameter subt. 90 |
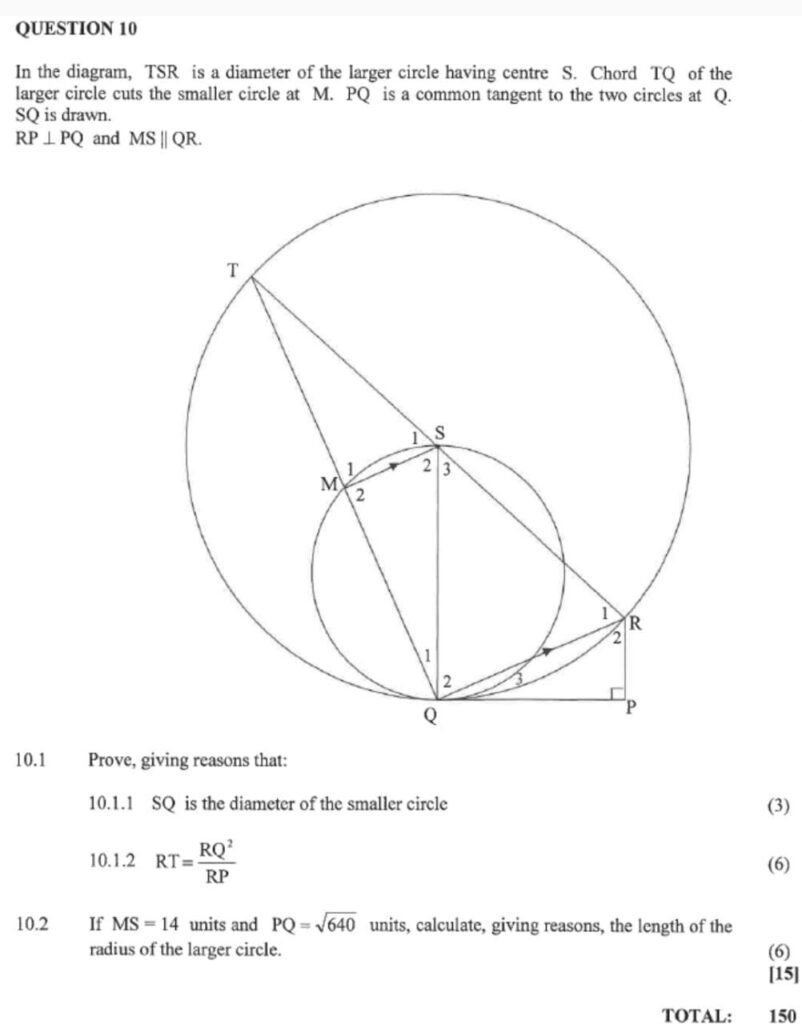
- from the above statement on our question:
- TSR is a diameter:
Conclusion: angle TQR is 90
- Centre S:
- S3 is an angle at centre, subtended by QR, equal to 2T, also subt. By QR
- S2 and s1 are also angles at centre, but are not subtended by anything in the larger circle
- TS, SR, QS are radii creating isosceles triangle TSQ and SQR
- MS is a line from centre to chord TQ, and bisects TQ using midpoint theorem (in triangle TQR, S is midpoint of TR and MS is parallel to QR, we can therefore conclude that M is also midpoint of TQ)
- Therefore, M1 and M2 are both 90
- Common tangent PQ:
- SQ is radius perpendicular to tangent PQ
- Q3 is angle between PQ and QR, QR subtends T, therefore T equals Q3
- We don’t have tangents from same point
- MS is parallel to QR
- Alt. angles S3 and Q2
- Corresponding angles R1 and S1, M1 and TQR
- Right angled triangle QRP
Where we will be able to use Pythagoras and/or trigonometry ratios
- NB: we therefore have exhausted our keywords and substantially highlighted our diagram as indicated below, and we can attempt questions without much difficulty.
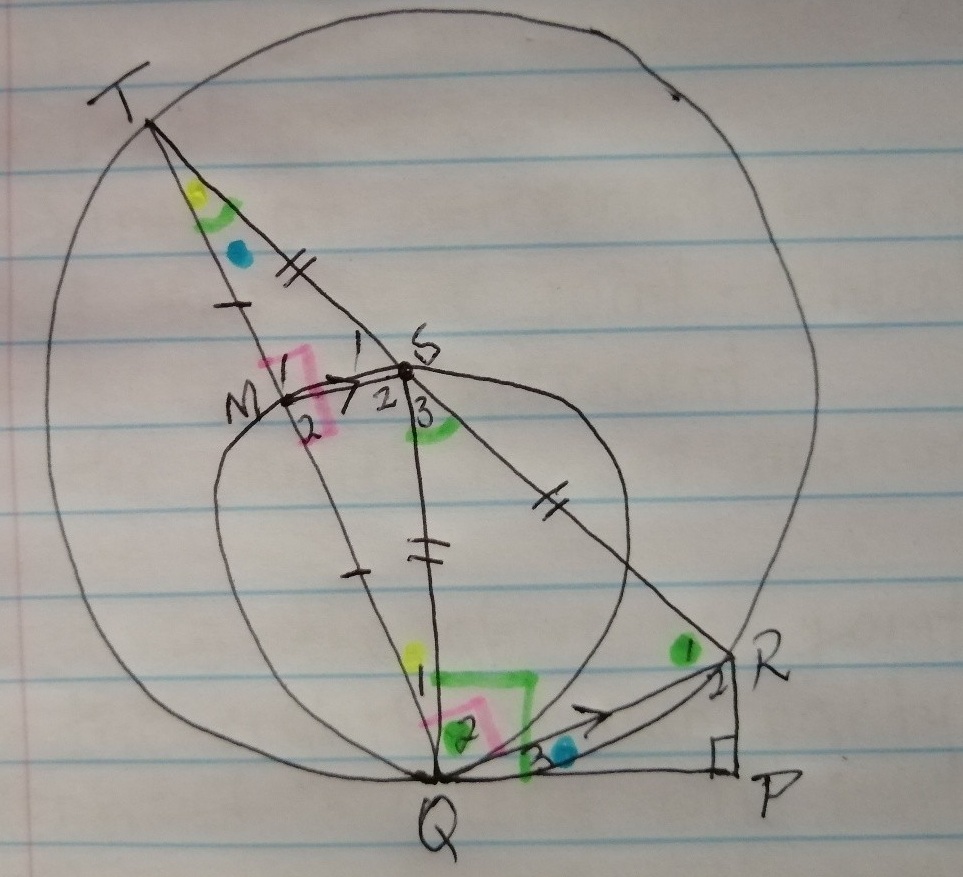
- ANSWERING:
10.1.1
S is midpoint of TR; MS is parallel to QR: Given
M is midpoint of TQ: midpoint theorem
M2 is 90: line from centre to midpoint
SQ is diameter: subtends 90 on M2
10.1.2
- The given equation comes from a proportion, RT/RQ=RQ/RP and was cross-multiplied to result in the given equation.
- So, we must assess in which triangles do those sides come from, make them similar, and the conclude the proportion. Cross multiply to get to the required.
- RT comes from triangle TRQ, RQ from triangle TRQ as well as from triangle SQR/RQP, RP from triangle QRP
- From the above we can see our common triangles as TRQ and QRP, then our job is to prove similarity in these triangles, get the proportion and cross multiply it.
Answer:
In triangle TRQ and QRP:
P equals 90: given
TQR equals 90: angle subt. By diameter
Therefore, P equals TQR
Q3 equals T: Tanchord theorem
R2 equals R1: third angle of a triangle
Triangle TQR is similar to QRP: AAA
NB: if we get two angles equal, the third one is always equal (third angle of a triangle)
RT/RQ=RQ/RP: proportionality
Cross multiply and get to the required
10.2
RT is the diameter of the larger circle, divided by 2 it will give the radius, and we can find RT using the equation from 10.1.2 question.
Our job is to find the size of RQ and RP
RQ is 28 units, 2x14: midpoint theorem
RP is 12 using Pythagoras in triangle QRP