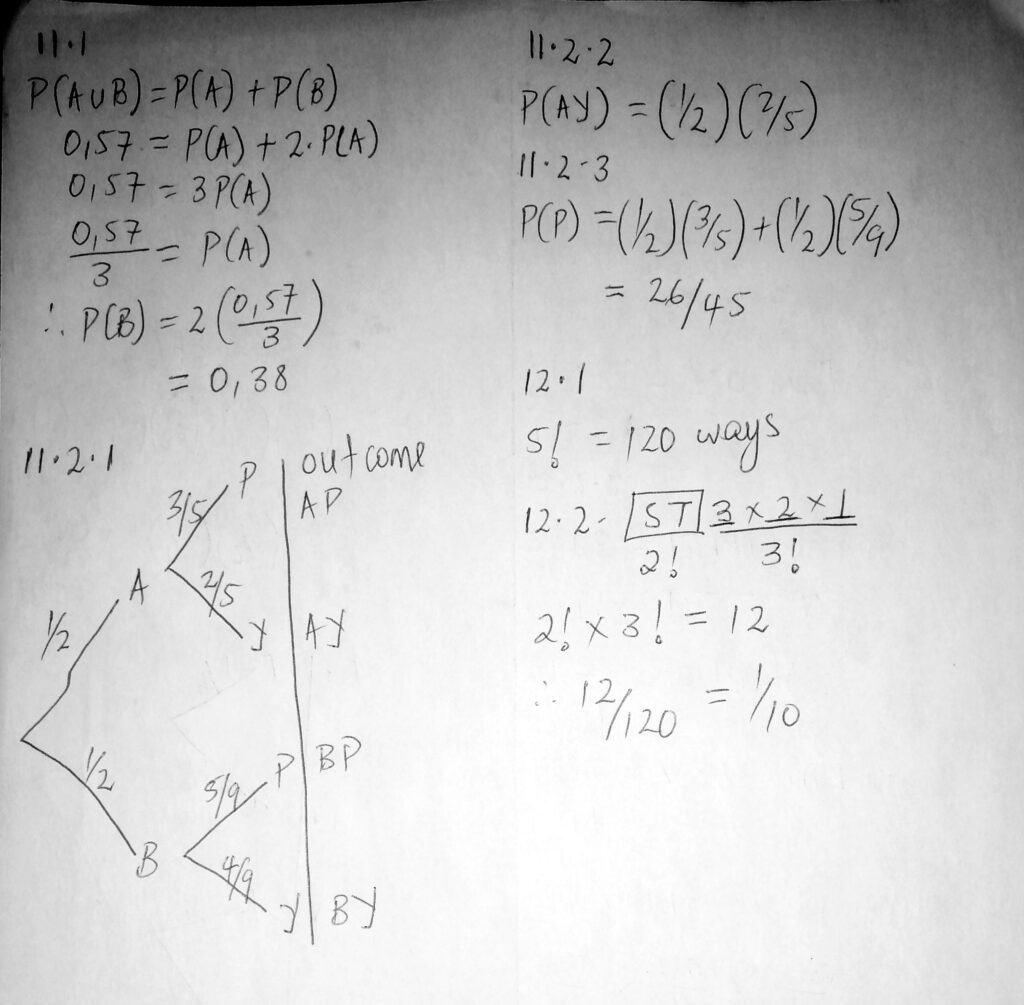Question:

11.1

Event A and B are mutual exclusive events

• This means they cannot occur at the same time
• The probability of the intersection, P(AnB), is zero

We’re further given properties we can use on the addition rule to provide an answer

• P(AuB)=P(A)+P(B)-P(AnB)
• But in this case the probability of event A and B occurring together is zero
• Therefore, the addition rule will be reduced to P(AuB)=P(A)+P(B)
• From here we can replace the given information and solve for probability of B as in the answer sheet bellow

11.2.1

Representing information, a tree diagram is tricky but simple, first time I did this I even drew it wrong.

The trick is to pay attention and place yourself in that situation, imagine you are there actually picking the pink and yellow ball from bag A or B

• It is given that we have two bags with equal probability, that is ½
• We can pic from bag A or B
• Myself I initially drew as if we are picking simultaneously, but the case is, we are picking from either bag, hence the ½ probability on our first two branches
• Bag A has a total of 5 balls, 3/5 pink and 2/5 yellow
• Bag B has 9 balls, 5/9 pink and 4/9 yellow
• The above two points make up our second branches as in the answer sheet
• Do not forget the most important part, the outcome

To identify probability using the outcome column

• Multiply probabilities across the branches
• And add the probabilities downwards on outcome

11.2.2

A yellow ball picked from bag A is A and Yellow, AY in our outcome

So, we multiply the probability of branch A and that of branch B

11.2.3

The probability of Pink is anywhere in our outcome where there is pink, P

That is, BP and AP

Multiply across the branches and add downwards

12.1

Given the word MATHS

We use factorial to find number of ways we can possibly arrange these letters

 ! is used as a factorial sign, found on casio calculator just below mode button

_ _ _ _ _

The above are empty spaces we have to fill using the 5 letters from the word MATHS

On first space we have 5 letters we can chose from, on second we have 4 since we have used 1 already, and then we have 3 letters left, then 2 and lastly 1

5x4x3x2x1

This can be written as 5! ,we have 5! Ways to arrange these letters

12.2

If S and T are to start, we therefore have fixed positions and can only make a choice on the last three letters

But we are not restricted on moving S and T, we can start we S or T, making it 2 arrangements

And then the last 3 we can arrange in 3!

Since we are asked probability, we must express our answer over total possible arrangements found on the first question above.

Answer: