Welcome to grade 12, holla matric!!!

Well, what most people do not notice is how much of grade 12 math is actually grade 11 math. That being said, I urge you to revisit grade 11 content posts every now and then, I will remind you in every grade 12 content post. This is the number one reason why we should get high marks; we cannot do one thing over and over again for two years and still underperform, noh mahn! Let’s kill this thing! Many have done it before you, you can do it and many will do it once again after you.

You see algebra, no one will teach will algebra in matric but your question paper is algebra everywhere. This is just an example of how important it is to revise your pre-matric content, matric is just a toping of the cake.

Sequence:

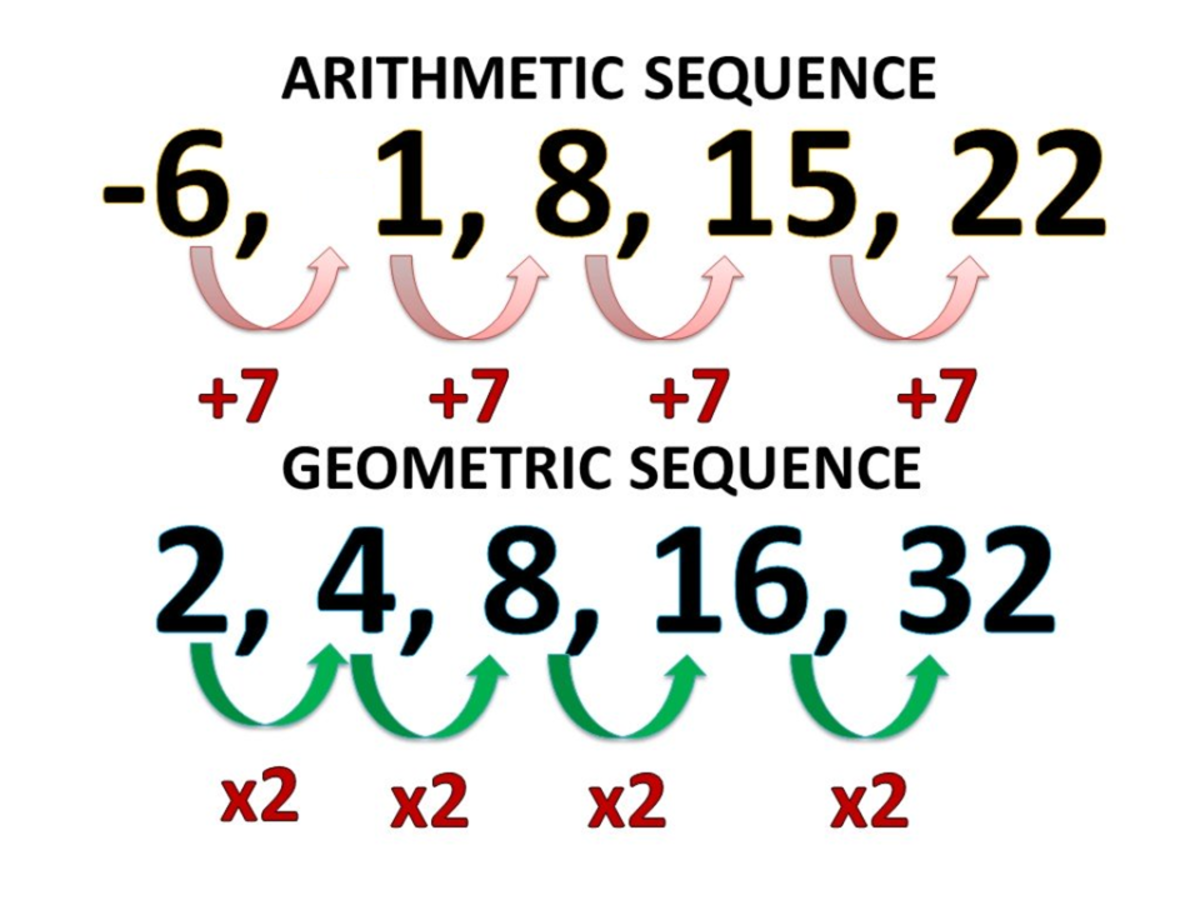
The same old linear and quadratic sequences from grade 11 will be examined and you should revisit them on the post available on grade 11 tab and your study guide.

In grade 12 they simple added geometric sequence:

• tn= ar^(n-1)
• a has always been the first term and yet again it is.
• R is the ratio between terms, found by dividing the second term with the first term or the fourth term with the third term.
• N has not changed, it’s the term number
• This sequence is more like the linear sequence, differing mainly by the nth term and the ratio; everything else is the same approach

Series:

This is a sequence but adding all the terms together, T1+T2+T3+…+Tn which will give us Sn (the sum of n terms). It can be divided into two types, being arithmetic series and geometric series, sharing the very same characteristics of the arithmetic and geometric sequence.

Arithmetic series:

You see the arithmetic sequence, 1;2;3;4;5;… for an example, add it together and you get an arithmetic series 1+2+3+4+5+…+Tn.

• Sn = (n/2)(2a+(n-1)d) or Sn = (n/2)(a+L)

Where:

Sn is the sum of n terms

N is the term number

A is always the first term

And d is also very much the same, difference.

L=Tn= a+(n-1)d

• The first formula is used when we do not know the last term, if we know the last term, we make use of the second formula to be quick and simple.
• These formulas will find the sum of the terms to whatever term number.

Geometric series:

These are the only apples we can actually compare to oranges, the geometric series is also an addition of terms just like the arithmetic series. The difference is d and r.

• Sn = (a(r^n -1))/r-1 or Sn = (a(1-r^n))/1-r

Where:

Sn is the sum of n terms

N is the term number

A is once again the first term

R is the ratio

• So, we make use of the first formula if r>1. The second formula is used where r<1

Sigma notation:

The sigma is use to express the sum of n terms, denoted by this sign ∑.

• Infront of the sigma we place the nth term
• The last term number is place right on top of the sigma sign
• And the first term number is place just below the sign.
• To find the number of terms: top number – bottom number +1

Sum to infinity:

Where the ratio is between 1 and negative 1, the geometric series tend to converge and will most likely never end. Its sum is the found using the following formula:

• Sum to infinity = a/(1-r)

And that’s it for the welcoming post, see you on the next one. Holla matric!

This blog post is not the first step towards learning the concepts of math but the coupling step to ease the use of your study guide and other study material. Read it over and over again to keep the concepts at the back of your head. Math is a subject of rules; know the rules, be able to duplicate them on a blank paper and go fetch your distinction